题目
552. 学生出勤记录 II
难度:困难
可以用字符串表示一个学生的出勤记录,其中的每个字符用来标记当天的出勤情况(缺勤、迟到、到场)。记录中只含下面三种字符:
'A':Absent,缺勤'L':Late,迟到'P':Present,到场
如果学生能够 同时 满足下面两个条件,则可以获得出勤奖励:
- 按 总出勤 计,学生缺勤(
'A')严格 少于两天。 - 学生 不会 存在 连续 3 天或 连续 3 天以上的迟到(
'L')记录。
给你一个整数 n ,表示出勤记录的长度(次数)。请你返回记录长度为 n 时,可能获得出勤奖励的记录情况 数量 。答案可能很大,所以返回对 109 + 7 取余 的结果。
示例 1:
输入:n = 2 输出:8 解释: 有 8 种长度为 2 的记录将被视为可奖励: "PP" , "AP", "PA", "LP", "PL", "AL", "LA", "LL" 只有"AA"不会被视为可奖励,因为缺勤次数为 2 次(需要少于 2 次)。
示例 2:
输入:n = 1 输出:3
示例 3:
输入:n = 10101 输出:183236316
提示:
1 <= n <= 105
方法一和方法二:我的动态规划+排列组合(+泰波纳契数列)
因为A的情况只有两种:一种是没有A,一种是有A,所以分开考虑。而有A的情况下,A只能有一个,所以考虑将这一个A分别放在字符串的所有位置,这样就将整个字符串分成了左右两个没有A的小部分。若用dp[i]记只有p和L组成的长度为i的字符串当中数量,那么带上A的总数就是将A放在每个位置上的时候dp[A左边长度]*dp[A右边的长度]的总和。而最前面考虑的整个字符串当中没有A的情况即为dp[总长度]。
所以接下来就是dp[i]的状态转移方程了。这里再建立两个状态,present[i]和late[i],分别用于表示长度为i时候以P和L开头(或结尾,其实一样的)的符合条件的数量。于是有状态转移方程:
present[i] = present[i-1]+late[i-1]
因为P可以既可以接在P后边,也可以接在L后边。late[i] = present[i-1]+present[i-2]
因为L可以接在两种情况后边:①恨着P;②只有一个L,这种时候就需要隔着一位是P了。dp[i] = present[i]+late[i]
这样就可以写代码了。初始状态可以人工算出。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23if n == 1:
return 3
if n == 2:
return 8
dp, late, present = [0]*(n+1), [0]*(n+1), [0]*(n+1)
# dp, late, present = {}, {}, {}
present[0] = late[0] = 1
present[1] = late[1] = 1
present[2] = late[2] = 2
dp[0], dp[1], dp[2] = 1, 2, 4
for i in range(3, n+1):
present[i] = present[i-1]+late[i-1]
late[i] = present[i-1]+present[i-2]
dp[i] = (present[i]+late[i]) % (10**9+7)
# print(present)
# print(dp)
ret = 0
for i in range(n):
t = dp[i]*dp[n-1-i]
ret += t % (10**9+7)
ret += dp[n]
return ret % (10**9+7)
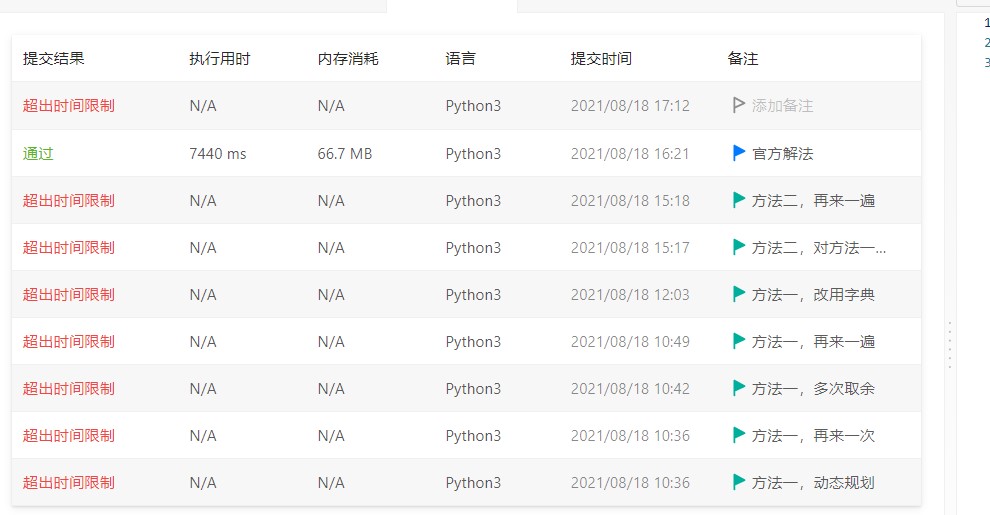
我以为我的思路那么简单清晰易懂,肯定没有问题(虽然确实可以解),但是提交之后超出时间限制了!以为因为中间没有每一步都取模(刚开始的时候没有)会导致大数运算变慢,于是每一步都加上取模运算;以为因为是列表取值慢于是有改成字典;以为网断了(其实并没有),重新连了网——而这些都没有用!
后来觉得可能是循环里头[]的取值操作有点多,于是将状态转移方程展开往下写,发现这里竟然有个泰波纳契数列。
dp[i]
= present[i]+late[i]
=present[i-1]+late[i-1]+present[i-1]+present[i-2]
=present[i-1]+(present[i-2]+present[i-3]) + present[i-1]+present[i-2]
=2present[i-1]+2present[i-2]+present[i-3]
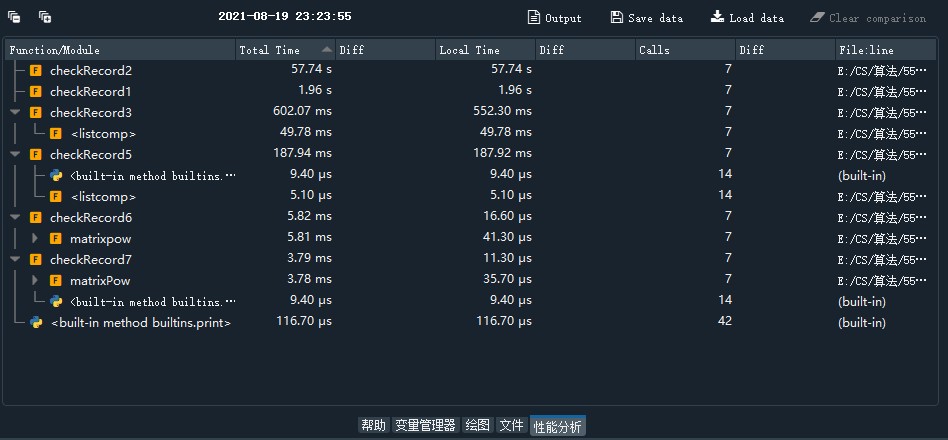
于是“改进”了方法的前面部分。然而仍然超时。——事实上这种更用时,后面放性能分析。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16def checkRecord2(n):
if n == 1:
return 3
if n == 2:
return 8
if n == 3:
return 19
# dp = [0]*(n+1)
dp = {}
dp[0], dp[1], dp[2], dp[3] = 1, 2, 4, 7
a, b, c = 1, 2, 4
for i in range(4, n+1):
dp[i] = a+2*b+2*c
a, b, c = b, c, a+b+c
...
方法三和方法四:官方的动态规划和我照官方的动态规划
1 | class Solution: |
借助他前面的讲解,也并没有很看懂,但了解了大概意思,然后理解着自己写了一个。
代码前面部分意思是列举所有情况,开头数字是dp下标。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33def checkRecord5(n):
# 0 前面没有A,现在要加P +=[0]+[1]+[2]
# 1 前面没有A,上一个不是L,现在要加L +=[0]
# 2 前面没有A,上一个是L,现在要加L +=[1]
# 3 前面有A,现在要加P +=[6]+[3]+[4]+[5]
# 4 前面有A,上一个不是L,现在要加L +=[6]+[3]
# 5 前面有A,上一个是L,现在要加L +=[4]
# 6 现在要加A +=[0]+[1]+[2]
MOD = 10**9+7
# dp = [[0 for _ in range(7)] for _ in range(n+1)]
# dp[1] = [1, 1, 0, 0, 0, 0, 1]
# for i in range(2, n+1):
# dp[i][0] += (dp[i-1][0]+dp[i-1][1]+dp[i-1][2])% MOD
# dp[i][1] += dp[i-1][0]% MOD
# dp[i][2] += dp[i-1][1]% MOD
# dp[i][3] += (dp[i-1][6]+dp[i-1][3]+dp[i-1][4]+dp[i-1][5])% MOD
# dp[i][4] += (dp[i-1][6]+dp[i-1][3])% MOD
# dp[i][5] += dp[i-1][4]% MOD
# dp[i][6] += (dp[i-1][0]+dp[i-1][1]+dp[i-1][2])% MOD
# return sum(dp[n])%MOD
dp = [[0 for _ in range(7)], [0 for _ in range(7)]]
dp[0][0] = 1
for i in range(1, n+1):
a, b = i % 2, 1-i % 2
dp[a][0] += (dp[b][0]+dp[b][1]+dp[b][2]) % MOD
dp[a][1] += dp[b][0] % MOD
dp[a][2] += dp[b][1] % MOD
dp[a][3] += (dp[b][6]+dp[b][3]+dp[b][4]+dp[b][5]) % MOD
dp[a][4] += (dp[b][6]+dp[b][3]) % MOD
dp[a][5] += dp[b][4] % MOD
dp[a][6] += (dp[b][0]+dp[b][1]+dp[b][2]) % MOD
dp[b] = [0]*7
return sum(dp[n % 2]) % MOD
这里其实也有两个方法,没注释掉的用上了滚动数组,这里需要注意的是清零的这一步dp[b] = [0]*7操作不能忘了。
方法五: 矩阵快速幂
有我前面列举过所有情况的基础上,写出矩阵快速幂就并不是那么难了。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36def checkRecord6(n):
mat = [
[1, 1, 1, 0, 0, 0, 0],
[1, 0, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 1, 1, 1],
[0, 0, 0, 1, 0, 0, 1],
[0, 0, 0, 0, 1, 0, 0],
[1, 1, 1, 0, 0, 0, 0]
]
MOD = 10**9+7
def multiply(a, b):
# a[r*m] * b[m*c] = ret[r*c]
r, m, c = len(a), len(a[0]), len(b[0])
ret = [[0 for _ in range(c)]for _ in range(r)]
for i in range(r):
for j in range(c):
for k in range(m):
ret[i][j] += a[i][k]*b[k][j]
ret[i][j] %= MOD
return ret
def matrixpow(mat, n):
ret = [[1], [0], [0], [0], [0], [0], [0]]
while n:
if n & 1:
ret = multiply(mat, ret)
mat = multiply(mat, mat)
n >>= 1
return ret
ret = matrixpow(mat, n)
ans = 0
for i in ret:
ans += i[0] % MOD
return ans % MOD