题目
- 出界的路径数
难度:简单给你一个大小为
m x n的网格和一个球。球的起始坐标为[startRow, startColumn]。你可以将球移到在四个方向上相邻的单元格内(可以穿过网格边界到达网格之外)。你 最多 可以移动maxMove次球。
给你五个整数 m、n、maxMove、startRow 以及 startColumn ,找出并返回可以将球移出边界的路径数量。因为答案可能非常大,返回对 109 + 7 取余 后的结果。
示例 1:
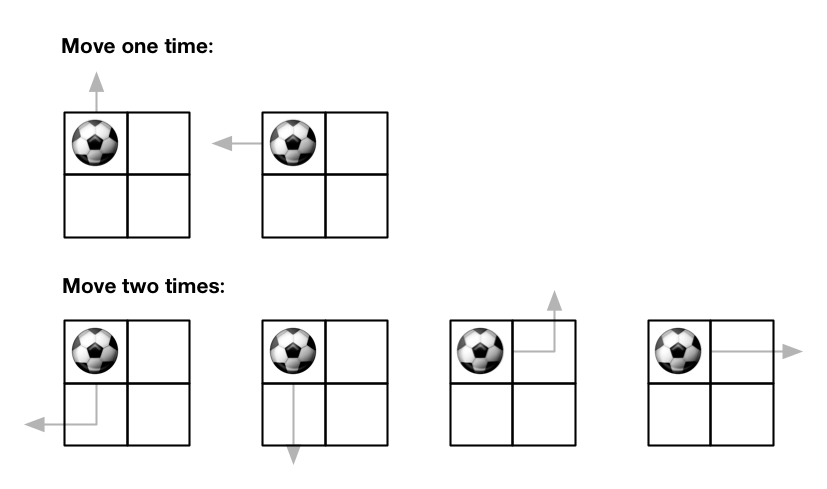
输入:m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0 输出:6
示例 2:
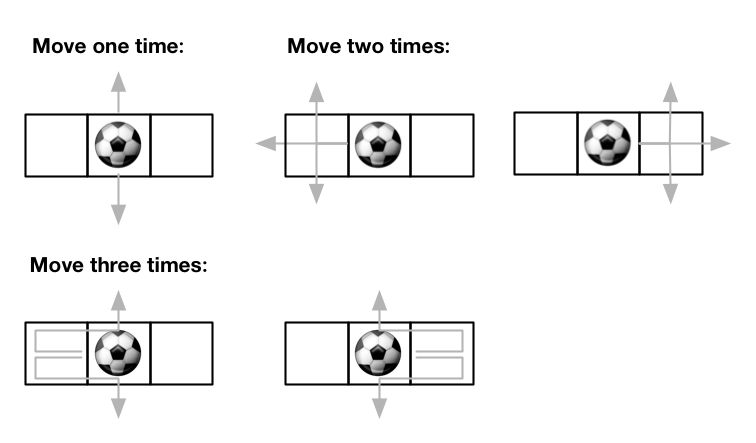
输入:m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1 输出:12
提示:
1 <= m, n <= 500 <= maxMove <= 500 <= startRow < m0 <= startColumn < n
f方法一: 动态规划
思路
这一题显然是要用动态规划来做。状态也不难写,dp[move][r][c]表示第move步走到第r行第c列的数量。状态转移方程也不难想到,即dp[move][r][c]等于move-1上一步步第r行第c列上下左右四个数的和,当然这是要在范围内,这里需要一个判断。而我的代码实现当中,是将这一步第r行第c列上下左右四个数加到下一步去。
较为复杂的我认为是在对于边界一圈的情况的考虑。如果球走到边界上了,剩余的步数至少还有一步,那他就可以出界,而且有多少种情况能走到边界的这个位置就有多少种出界的情况。但就如题目中的示例那样,边界的不同位置出界的可能i性是不同的。所以,我是在循环当中,先判断这个位置是不是边界以及是哪一种边界,如果是,再判断这个位置上是不是0,如果不是0,说明可以出界,那就将它加到出界总数去,一种边界加一次,这样就解决了边界不同位置有不同出界的可能性。
代码
1 | def findPaths(m, n, maxMove, startRow, startColumn): |
方法二: 卷积
大佬都在评论区。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18def findPaths(m, n, maxMove, startRow, startColumn):
if maxMove <= 0:
return 0
ans = 0
a = numpy.zeros((m, n), )
a[startRow, startColumn] = 1
b = numpy.zeros((3, 3), int)
b[0][1] = b[1][0] = b[-1][1] = b[1][-1] = 1
# print(a)
for _ in range(maxMove):
ans += (a[:, 0].sum() + a[:, -1].sum() +
a[0, :].sum() + a[-1, :].sum()) % 1_000_000_007
a = scipy.signal.convolve2d(a, b, 'same') % 1_000_000_007
print(a)
return int(ans) % 1_000_000_007