题目
1719. 重构一棵树的方案数
难度:困难
给你一个数组 pairs ,其中 pairs[i] = [xi, yi] ,并且满足:
pairs中没有重复元素xi < yi
令 ways 为满足下面条件的有根树的方案数:
- 树所包含的所有节点值都在
pairs中。 - 一个数对
[xi, yi]出现在pairs中 当且仅当xi是yi的祖先或者yi是xi的祖先。 - 注意:构造出来的树不一定是二叉树。
两棵树被视为不同的方案当存在至少一个节点在两棵树中有不同的父节点。
请你返回:
- 如果
ways == 0,返回0。 - 如果
ways == 1,返回1。 - 如果
ways > 1,返回2。
一棵 有根树 指的是只有一个根节点的树,所有边都是从根往外的方向。
我们称从根到一个节点路径上的任意一个节点(除去节点本身)都是该节点的 祖先 。根节点没有祖先。
示例 1:
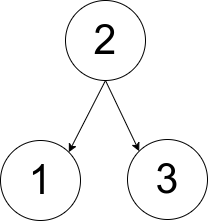
输入:pairs = [[1,2],[2,3]] 输出:1 解释:如上图所示,有且只有一个符合规定的有根树。
示例 2:

输入:pairs = [[1,2],[2,3],[1,3]] 输出:2 解释:有多个符合规定的有根树,其中三个如上图所示。
示例 3:
输入:pairs = [[1,2],[2,3],[2,4],[1,5]] 输出:0 解释:没有符合规定的有根树。
提示:
1 <= pairs.length <= 1051 <= xi < yi <= 500pairs中的元素互不相同。
思考过程
一开始一直看不懂题目,不明白示例三为什么不行,认为示例三很容易就能画出一棵树来。反复读题之后才意识到题目中“树所包含的所有节点值都在 pairs 中。”的意思,就是说构造出来的树的所有信息都要再pairs中体现,也明白了为什么要那样输出,只要找到符合条件的2个就能输出了。
于是看示例三就能想到:如果一个节点在一个数对中做了孩子节点,那它在其他数对中只能作为双亲节点,比如示例三中的2节点。
不对不对,;pairs[i] = [xi, yi] 中,xi和yi之间的关系是祖先和后代的关系,而不是双亲孩子的关系,所以这不能用来解题。
那也就是说所有祖先后代的关系在pairs当中都有体现,那如果存在根节点的话,每一组数对当中都会有这个根节点咯?——找到根节点了!
呀,不是在每个数对中都出现,就是:
d = defaultdict(set)
for x,y in pairs:
d[x].add(y)
d[y].add(x)
这样d[根节点]就包含了除自己以外所有的节点,而d[x]就是包含x的所有祖先和后代了。
然 后呢?官解是直接模拟,模拟啥呀?xi < yi这个条件有什么用吗?应该没有吧,只是一种表示而已吧。
能不能再统计一下d[x]的个数,然后用集合的相关运算划分出不同的子树,然后……
哎,大约只能想到这了,看官解吧。
哎,官解前面设的东西和我的想法好像哦。
看了一圈题解,字面上的也基本上都懂了,但离理解还是差点。
自己写了一个。
1 | class Solution: |
将某个节点的所有祖先和所有后代还有它自己装进一个集合里,然后以集合大小为排序依据进行排序。从小的开始,找到包含这个小集合的最小的大集合,那个就是小集合对应的节点的父节点了。然后判断如果这两集合一样大,那就说明可以交换。
这样是错误的,问题在于,所有集合都是根节点的那个集合的子集,那所有节点都能认根节点作为它的直接父节点。完了。
看官解代码:
1 | from sys import maxsize |
其中# #是我的注释。
现在问题就是,
# 检测 neighbours 是否为 adj[parent] 的子集
# # if parent == -1 or not neighbours.issubset(adj[parent]):
if parent == -1 or any(neighbour != parent and neighbour not in adj[parent] for neighbour in neighbours):
return 0
我用集合本身的判断是否为另一个集合的子集的函数,结果是错误的。
现在就是要重点理解any(neighbour != parent and neighbour not in adj[parent] for neighbour in neighbours)了。还有,parent什么时候会是-1呀?
不,在这里parent都不可能是-1,经代码提交确认也是这样。
any(neighbour != parent and neighbour not in adj[parent] for neighbour in neighbours)
any()只要有一个是True,结果就是True。- 遍历当前
node的neighbours,若出现一个节点不属于parent那个集合时,就可以证明这个parent不是这个node的父节点:- 当遍历的
neighbour不是parent(neighbour != parent为True)时,neighbour又不在parent的集合里,整体值为True,即parent不是当前node的父节点,return 0; - 当遍历的
neighbour恰好时parent(neighbour != parent为False)时,neighbour也一定不在’parent的集合里,因此整体值为False`;
- 当遍历的
好家伙,总算是理清了。

